log in
Active Users
Feedback
About and Contact
© 2020 DOUBTCOOL
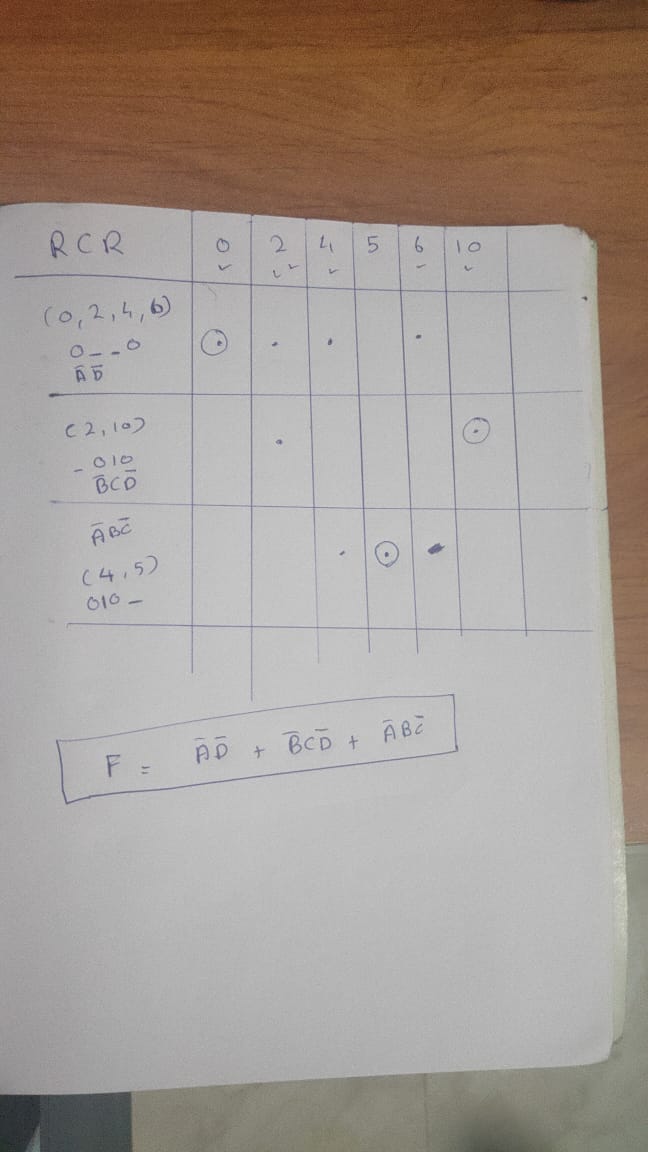
The given min terms are arranged into 4 groups based on the number of ones
present in their binary equivalents. Arrange the given min terms in an ascending
order and make the groups based on the number of ones present in their binary
representations. So, there will be at most ‘n+1’ groups if there are ‘n’ Boolean
variables in a Boolean function or ‘n’ bits in the binary equivalent of min terms.
Compare the min terms present in successive groups. If there is a change in only
one-bit position, then take the pair of those two min terms. Place this symbol ‘_’
in the differed bit position and keep the remaining bits as it is. Formulate
the prime implicant table. It consists of set of rows and columns. Prime
implicants can be placed in row wise and min terms can be placed in column
wise. The given Boolean function is in sum of min terms form. It is having 4
variables A, B, C & D. Using tabulation method, compute the total number of
prime implicants of the following function and minimize it
F(A, B, C, D) = ∑m (0, 2, 4, 5, 6, 10)
present in their binary equivalents. Arrange the given min terms in an ascending
order and make the groups based on the number of ones present in their binary
representations. So, there will be at most ‘n+1’ groups if there are ‘n’ Boolean
variables in a Boolean function or ‘n’ bits in the binary equivalent of min terms.
Compare the min terms present in successive groups. If there is a change in only
one-bit position, then take the pair of those two min terms. Place this symbol ‘_’
in the differed bit position and keep the remaining bits as it is. Formulate
the prime implicant table. It consists of set of rows and columns. Prime
implicants can be placed in row wise and min terms can be placed in column
wise. The given Boolean function is in sum of min terms form. It is having 4
variables A, B, C & D. Using tabulation method, compute the total number of
prime implicants of the following function and minimize it
F(A, B, C, D) = ∑m (0, 2, 4, 5, 6, 10)
2 regular answers available